Improving user experience : AB Testing changes

We will be using statistical tools to validate improvements in the retention rate of our app

Data source : https://www.kaggle.com/yufengsui/mobile-games-ab-testing

Problem Description

Imagine we have developed a mobile application and we are want to improve the retention of our app,it is a mobile game where they encounter gates that forces them to wait a certain amount of time, or make an in-app purchase to progress. This is a way to encourage user spending and also to increase the usage and retention of the game, but where should the gate be placed?

The users are divided in two groups:

• Group A with the gate at level 30
• Group B with the gate at level 40

We want to find if it is better to place the gate at level 30 or level 40, we do this by recording:

• userid : Unique key assigned to each user
• sum_gamerounds : The number of rounds played by the player 14 days after the install
• retention_1 : Did the player come back and play 1 day after installing?
• retention_1 : Did the player come back and play 7 days after installing?

Import Data

import pandas as pd
import numpy as np
import pymc3 as pm
import plotly.graph_objects as go
import arviz as az

data = pd.read_csv("cookie_cats.csv",index_col = 0)
display(data.head(5))

Let’s check for missing data:

display("Missing values : "+ str(sum(data.isnull().values)))

'Missing values : [0 0 0 0]'

Split the dataset into A and B groups

a = data[data["version"] == "gate_30"]
b = data[data["version"] == "gate_40"]

A/B Testing

Testing 1 day retention

To find out the group that has better retention we use AB testing to find if there is a statistically significant difference between the two groups, in particular, we want to consider the following random variables:

In short:

Where X is the event “user coming back 1 day after installation” and can take a true or false value.

What we are really interested in is \(p_A\) and \(p_B\) which are the probabilities of the user coming back being true:

\(p_A\) and \(p_B\) are what we call the Retention Rate of putting the gate at level 30 and putting the gate at level 40

To estimate \(p_A\) and \(p_B\) we will use the Bayesian inference with PyMC3 which is a python package for Bayesian statistical modeling and probabilistic machine learning which focuses on advanced Markov chain Monte Carlo (https://docs.pymc.io/).

We want to test with a significance level = 0.05 if the retention rate of B is greater than group A, thus we test the null hypothesis that with:

Against the alternative hypothesis:

We also want to calculate the relative change from group A to group B:

• First we consider \(p_A\) and \(p_B\) to be random continuous variables in the interval [0,1] Beta distributed (this is our prior)
• We sample from our data and estimate \(p_A\),\(p_B\)
• Evaluate D and R.
• Repeat for multiple times (10000)
• In the end we will have the distributions of our parameters \(p_A\),\(p_B\) and their absolute and relative difference.
• Finally we check the p-value of \(D \leq 0\), if it is greater than 5%, we reject the hypothesis that there has been an improvement in the 1 day retention after moving the gate (we accept the null).

with pm.Model():
    a_p = pm.Beta("a_p",1,1)
    b_p = pm.Beta("b_p",1,1)
    a_bin = pm.Bernoulli("a bernoulli",p = a_p,observed = a["retention_1"])
    b_bin = pm.Bernoulli("b bernoulli",p = b_p,observed = b["retention_1"])
    difference = pm.Deterministic("1 day retention difference",b_p-a_p)
    rel_difference = pm.Deterministic("1 day retention relative difference",(b_p-a_p)/a_p)
    trace = pm.sample(10000, tune=1000, cores = 4)
    pm.plot_density([trace.get_values("a_p"),trace.get_values("b_p")],credible_interval = 1.0,data_labels=["a_p","b_p"],shade=.8)
    pm.plot_posterior(trace,var_names = ["1 day retention difference","1 day retention relative difference"],credible_interval = None,ref_val = 0,round_to = 6)
    display(pm.summary(trace,credible_interval = 0.98)[["mean","sd","hpd_1%","hpd_99%"]])

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [b_p, a_p]
Sampling 4 chains, 0 divergences: 100%|██████████| 44000/44000 [01:39<00:00, 440.61draws/s]

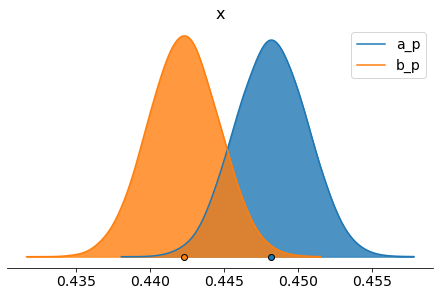
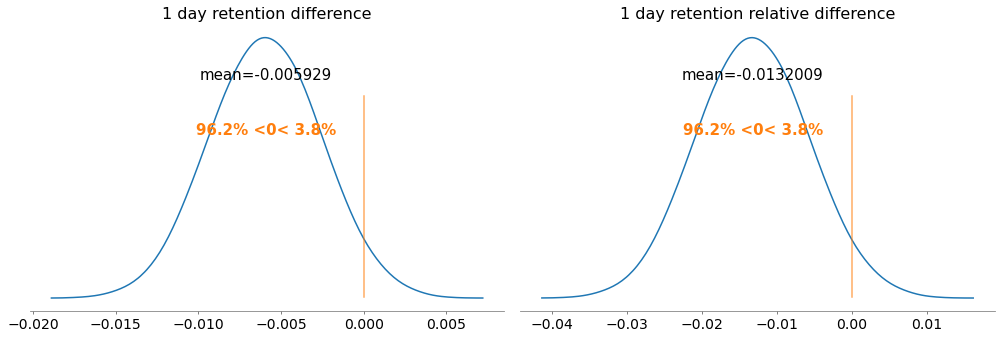
Here we can see that the probability of our null hypothesis being true is 96.2% (this is our p-value, bigger than our significance level of 5%), thus we can say that moving the gate to level 40 does not improve our 1 day retention, accepting the null hypothesis, with a mean decrease in retention rate of 0.5%, which is around 1.3% worse than leaving it at level 30

Testing 7 day retention

Now we apply the same reasoning written above to evaluate the change in the 7 days retention given the same null hypothesis and the same significance level

with pm.Model():
    a_p = pm.Beta("a_p",1,1)
    b_p = pm.Beta("b_p",1,1)
    a_bin = pm.Bernoulli("a bernoulli",p = a_p,observed = a["retention_7"])
    b_bin = pm.Bernoulli("b bernoulli",p = b_p,observed = b["retention_7"])
    difference = pm.Deterministic("7 day retention difference",b_p-a_p)
    rel_difference = pm.Deterministic("7 day retention relative difference",(b_p-a_p)/a_p)
    trace = pm.sample(10000, tune=1000, cores = 4)
    pm.plot_density([trace.get_values("a_p"),trace.get_values("b_p")],credible_interval = 1.0,data_labels=["a_p","b_p"],shade=.8)
    pm.plot_posterior(trace,var_names = ["7 day retention difference","7 day retention relative difference"],credible_interval = None,ref_val = 0,round_to = 6)
    display(pm.summary(trace,credible_interval = 0.98)[["mean","sd","hpd_1%","hpd_99%"]])

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [b_p, a_p]
Sampling 4 chains, 0 divergences: 100%|██████████| 44000/44000 [01:23<00:00, 524.56draws/s]

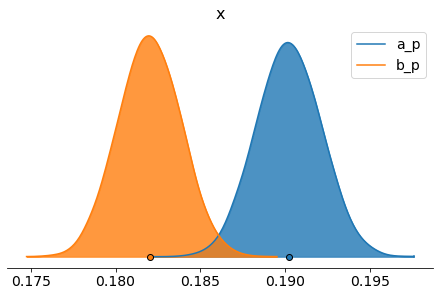
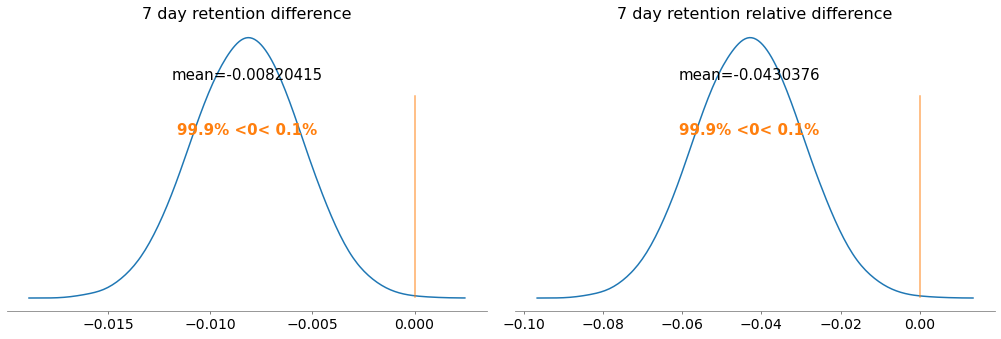
Here the evidence is even stronger, we have a p-value of 99.9%, much bigger than our 5% threshold, again we accept \(H_0\).

With a mean decrease in retention rate of around 0.8%, which is around 4.3% worse than leaving it at level 30, we conclude that moving the gate at level 40 does not improve our 7 days retention.

Testing the number of gamerounds played

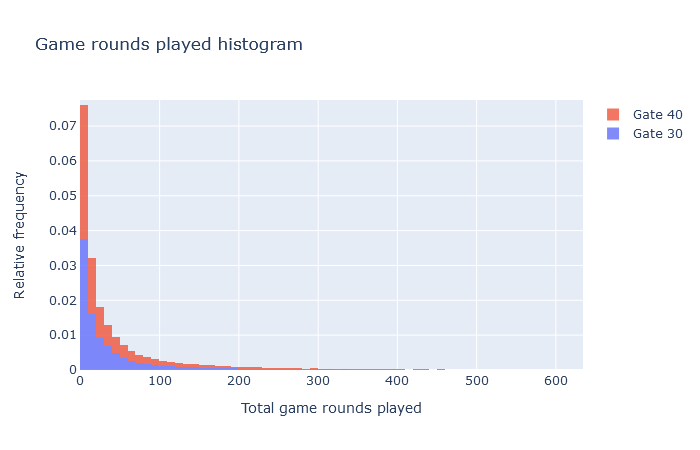
Now we want to test if there is a significant difference in the number of game-rounds played, given that we don’t know the distribution of the game-rounds played, we take a look at the histograms of the two groups:

fig = go.Figure(go.Histogram(x = a["sum_gamerounds"],histnorm="probability density",name = "Gate 30",nbinsx = 7000))
fig.add_trace(go.Histogram(x = b["sum_gamerounds"],histnorm="probability density",name = "Gate 40",nbinsx = 7000))
fig.update_traces(opacity=0.8)
fig.update_layout(barmode="stack",
                  title="Game rounds played histogram",
                  xaxis_title="Total game rounds played",
                  yaxis_title="Relative frequency",)
fig.show()

We model the number of game-rounds played as a negative binomial random variable X:

\(μ_A\) and \(μ_B\) are the means of the distributions and \(α_A\),\(α_B\) their shape parameters

We want to test the difference of the means between group B and A with a significance level of 0.05:

And calculate relative change from A :

We choose an Exponential prior for \(μ_A\) and \(μ_B\)

with pm.Model():
    a_mean = pm.Exponential("a mean",lam = 1/a["sum_gamerounds"].mean())
    b_mean = pm.Exponential("b mean",lam = 1/b["sum_gamerounds"].mean())
    a_alpha = pm.Gamma("a alpha",1,1)
    b_alpha = pm.Gamma("b alpha",1,1)
    a_distribution = pm.NegativeBinomial("a distrib",mu = a_mean,alpha = a_alpha)
    b_distribution = pm.NegativeBinomial("b distrib",mu = b_mean,alpha = b_alpha)
    a_gamma = pm.NegativeBinomial("a exp",mu = a_mean,alpha = a_alpha,observed = a["sum_gamerounds"])
    b_gamma = pm.NegativeBinomial("b exp",mu = b_mean,alpha = b_alpha,observed = b["sum_gamerounds"])
    difference = pm.Deterministic("mean gameround difference",b_mean-a_mean)
    rel_difference = pm.Deterministic("mean gameround relative difference",(b_mean-a_mean)/a_mean)
    trace = pm.sample(10000, tune=1000, cores = 4)
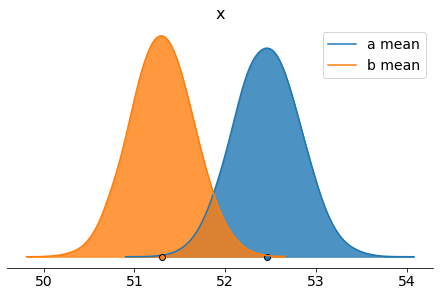
    pm.plot_density([trace.get_values("a mean"),trace.get_values("b mean")],credible_interval = 1.0,data_labels=["a mean","b mean"],shade=.8)
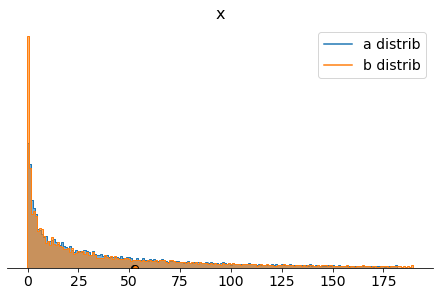
    pm.plot_density([trace.get_values("a distrib"),trace.get_values("b distrib")],data_labels=["a distrib","b distrib"],shade=.6)
    pm.plot_posterior(trace,var_names = ["a distrib","b distrib"],credible_interval = None,round_to = 6)    
    pm.plot_posterior(trace,var_names = ["mean gameround difference","mean gameround relative difference"],credible_interval = None,ref_val = 0,round_to = 6)
    display(pm.summary(trace,credible_interval = 0.98).loc[["a mean","b mean","mean gameround difference","mean gameround relative difference"]][["mean","sd","hpd_1%","hpd_99%"]])

Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>NUTS: [b alpha, a alpha, b mean, a mean]
>CompoundStep
>>Metropolis: [b distrib]
>>Metropolis: [a distrib]
Sampling 4 chains, 0 divergences: 100%|██████████| 44000/44000 [18:12<00:00, 40.28draws/s]
The number of effective samples is smaller than 10% for some parameters.

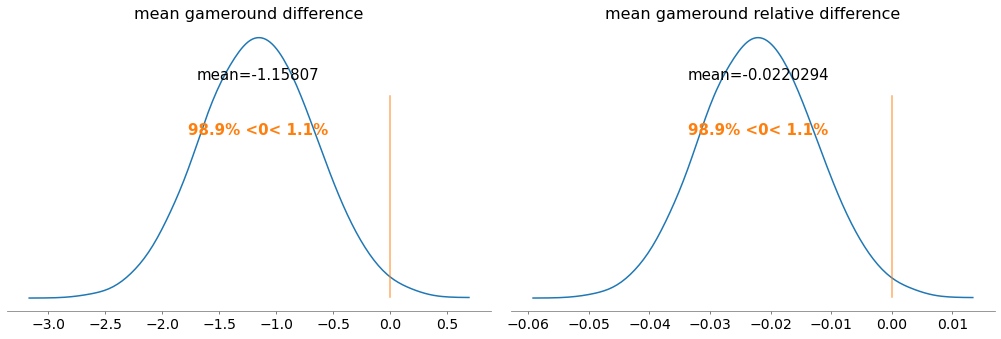
Again, same reasoning, the difference of means is around -1.16, 2.2% worse, p-value = 98.9%, bigger than our confidence level of 5% (let’s remember one more time that in order to refuse the null hypothesis the probability of the mean difference being less or equal than 0 must be less or equal than our confidence level).

We conclude that moving the gate does not improve the number of rounds played.

Should we implement the change?

Given the data we collected and the effects of our decision on the indicators we analyzed, it is safe to say that moving the gate to level 40 worsens our 1 day and 7 days retention and the number of rounds played.

This can be explained in a well known phenomena in the entertainment industry called “hedonic treadmill”, by playing and generating a sense of happiness in the user, it needs more and more entertainment to keep the user at that state, otherwise, he will get bored.

By forcing the user to take a break earlier (with the gate mechanic we explained at the beginning at level 30 instead of 40), we avoid the user getting bored by the game and keep him coming back.

• 2020 3
• 2019 1