Single facility location problem

In this post we will find out how to choose the best location for a single uncapacitated facility given a set of points of interest

Code and data used: https://github.com/davbom97/source

Problem description

Suppose we pose ourselves the following problem: given some known factors, where should we build our facility (a supermarket, a shop, a distribution center, etc.) so we maximize our profits.
This is a common question that must be asked every time we plan to make an investment to expand a business in a new region. Besides, often the available data might be the bare minimum, so we must make assumptions and make the most out of the data.

In this case, our problem is the following : we want to build a new supermarket in the province of Brescia, Italy. The only data given is :

• The cities in the province
• Their population
• Their georaphical location (latitude and longitude) We will try to find the optimal location to build our new supermarket.

In our solution we are making the following hypotheses:

1. All the costs are assumed the same for every place, which means that the only relevant cost is the transportation cost, proportional to the distance between the facility and each town.
2. We don’t have data on the clients, so we weigh our decision based on the total population of each region.
3. The supermarket alone can supply all the possible demand, so it is necessary to build one and only one facility.

Data Retrieval

First we import the relevant libraries and the cities data (from the year 2011)

import pandas as pd
from geopy.geocoders import Nominatim
import numpy as np
from scipy import optimize as opt
from IPython.display import display
import time

data = pd.read_excel("Brescia_province_data.xlsx",sep = ";")
display(data.head(10))

Now we need to get the latitudes and longitudes of the cities to compute the distances,we do so using a geolocator:

geoloc = Nominatim(user_agent="Facility_loc_problem")
coordinates_df = pd.DataFrame(np.zeros((len(data.index),2)),index = data.index, columns = ["lat","long"])
cities = data.loc[:,"City"].values
i = 0
while i != (len(cities)): #gets the latitude and longitude of every city
    try:
        location = geoloc.geocode(cities[i] + ", Brescia, Italy")
        coordinates_df.loc[i,"lat"] = location.latitude 
        coordinates_df.loc[i,"long"] = location.longitude
        i+=1
        time.sleep(1)
    except:
        time.sleep(20)
        continue
data = data.join(coordinates_df)

Now let’s see the updated dataframe with the coordinates of each city:

data.to_csv("Brescia_province_data_complete.csv",sep = ";")
display(data)

Here are all the cities plotted on a map:

Solving the problem

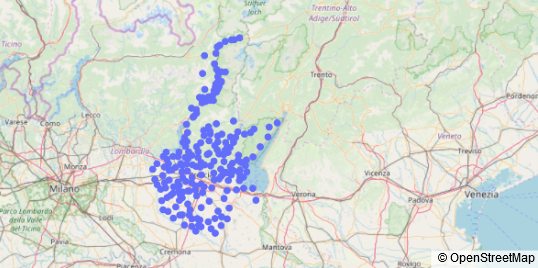
Now that we have acquired all the necessary data, we can start describing the distance, the distance I’ve chosen is the rectilinear (also called “Manhattan”) distance of the latitudes and longitudes, due to the fact that is more realistic than the euclidean distance and takes into account for multiple possible paths to reach a city, the formula is:

\(d_i\) = rectilinear distance between the location the i-th point
\(x\) = latitude of our facility
\(y\) = longitude of our location
\(x_i\) = latitude of the i-th city
\(y_i\) = longitude of the i-th city

then we weigh each distance by a factor \(w_i\)

our weight in this case is the city population

now we can write the sum of weighted distances between the facility and the points as:

and so our objective function will be:

Now we will write the code that will find the values x,y of our location so that the sum of weighted distances is minimized:

def objective_func(location,points_coords,points_weights):
    x = location[0]
    y = location[1]
    x_i = points_coords[:,0]
    y_i = points_coords[:,1]
    w_i = points_weights
    return sum((abs((x_i-x))+abs((y_i-y))*w_i))
location = [0,0] #our starting latitude and longitude for the facility
coordinates_df = data.loc[:,["lat","long"]]
res = opt.minimize(objective_func,location,args = (coordinates_df.values, data.loc[:,"Pop size"].values),method ="Nelder-Mead",tol = 10**(-9))
location = res.x
print("The latitude and the longitude of the optimal location is = " + str((res.x[0],res.x[1])))

The latitude and the longitude of the optimal location is = (45.539802200000004, 10.267566991613718)

Visualizing our result

Now that we’ve got the latitude and longitude of the optimal location we can get its address and plot it on the map:

print(geoloc.reverse(location))

Quartiere Colonnello Gherardo Vaiarini, Concesio, Comunità montana della valle Trompia, Brescia, Lombardia, 25062, Italia

Analyzing the result

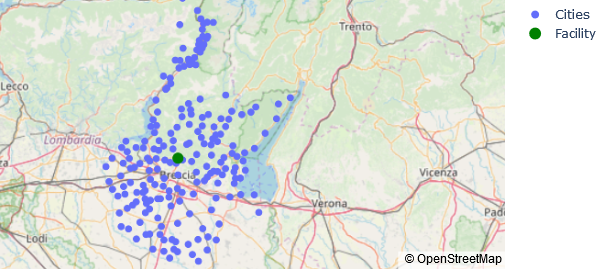
The method provides the best location to minimize the average distance between the location and the clients,this is why we take in account the population size (it would be best if we knew the number of clients in each city but it is a necessary approximation in case we have no data) and also minimizes the average travel time.

In case we have a set of locations to choose for our facility, the problem becomes trivial, in fact, with a few adjustments we can take into account the investment necessary to build in a specific location, this will be subject to another work.

A non-trivial problem is the multiple facility problem, which will require an approximate solution through clustering.

It is important to point out that this method is general-purpose whenever our problem requires to minimize the distance between a point and a set of other points (whatever and wherever they could be).

• 2020 3
• 2019 1